Set language and notation
Sets allow us to group different things (they could letters, numbers even objects) together and study them by finding similarities or differences in them and how they behave. In many ways it’s patterns along with similarities and differences.
Requirements
- Understanding of KS3.
Delving into the topic…
A set is a collection of distinct objects. These objects can be also known as elements or members. In the world of sets we also have the idea of an entire universe or a “master set” which contains every single object of each set. This set is known as the universal set. However, there is also a set which contains no objects known as the empty set.
Here are some examples of sets:
$$ \xi: 1,2,3,4,5,6,7,8,9,10,11,12 $$ $$ A: \text{multiples of 3} $$ $$ B: \emptyset $$ $$ C: \text{multiples of 5} $$
The top set is the symbol for the universal set, set B has the symbol for no objects; it is an empty set.
The union of sets is every object in either set. For example:
$$ A \cup C = \text{(multiples of 3)} \cup \text{(multiples of 5)} = 3,6,9,12 \cup 5,10 $$ $$ \therefore A \cup C = 3,5,6,9,10,12 $$
The intersection of sets is every object in all sets:
$$ A \cap \xi = \color{red}{3},6,9,12 \cap 1,2,\color{red}{3},4,5,\color{red}{6},7,8,\color{red}{9},10,11,\color{red}{12} $$ $$ A \cap \xi = 3,6,9,12 = A $$
We can also place objects in a set manually or say that they are not in a set like this:
$$ 3 \in A, 5 \notin B $$
The complement of a set is everything that is not in the set. For example:
$$ (A \cap \xi)^{\complement} = (3,6,9,12)^{\complement} = 1,2,4,5,7,8,10,11 $$
A comma can also be used to show the complement of a set. We can represent the set operations we’ve learnt through venn diagrams:
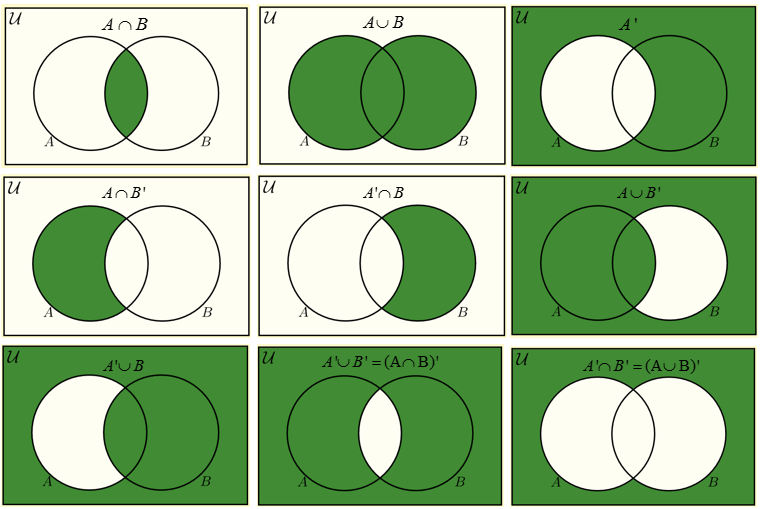
If we were to arrange each set and the universal set into containers where the outside represents everything, the inside of a container represents all the objects of that set and there is an overlap where objects that fit into both sets go, we can make a venn diagram to visualise set operations. On the above image, the green represents where the objects of the answer are located.
A very simple operation we can do on sets is to determine the number of objects in a set. For example:
$$ n(A \cap \xi) + n(A \cup C) = 8 + 6 = 14 $$
Subsets are sets contained inside of bigger sets. In other words a subset of a set contains all of the objects that the set contains. For example:
$$ D \subset C $$
means that all of the elements of set D must be elements of set C. So all the elements of set D must be multiples of 5.
Further reading
- More coming soon…
Home - Maths Portal
This work is licensed under a Creative Commons Attribution-NoDerivatives 4.0 International License..